John Taylor complains that the kalam cosmological argument gives the appearance of being a swift and simple demonstration of the existence of a Creator of the universe, whereas in fact a convincing argument involving the premiss that the universe began to exist is very difficult to achieve. But Taylor's proffered defeaters of the premisses of the philosophical arguments for the beginning of the universe are themselves typically undercut due to Taylor's inadvertence to alternatives open to the defender of the kalam arguments. With respect to empirical confirmation of the universe's beginning Taylor is forced into an anti-realist position on the Big Bang theory, but without sufficient warrant for singling out that theory as non-realistic. Therefore, despite the virtue of simplicity of form, the kalam comological argument has not been defeated by Taylor's all too swift refutation.
"A Swift and Simple Refutation of the Kalam Cosmological Argument?" Religious Studies 35 (1999): 57-72.
I. Introduction
In his helpful book God, Reason, and Theistic Proofs, Stephen T. Davis explores at some length what criteria must be fulfilled by a theistic argument in order for it to count as a successful piece of natural theology. Of course, the argument must be formally and informally valid; moreover, Davis opines, its premisses must be known to be more plausible than their denials.{1} When assessed by this standard, it seems to me that the kalam cosmological argument qualifies as a successful piece of natural theology, for it is obviously valid, and we may at least know that its premisses are more plausible than their denials, even if we do not know them to be necessarily true, or simply true, or even plausible.
John Taylor disagrees.{2} The kalam cosmological argument cannot in his view be endorsed because its adherents have not shown its main premiss, that the universe began to exist, to be more reasonable than its denial.
Taylor's fundamental complaint is that the kalam cosmological argument gives the appearance of providing a swift and simple demonstration of the existence of a supernatural Creator of the universe, whereas in fact a convincing argument for such a conclusion would have to be much more complicated and laborious than a single syllogism. This seems a strange complaint to lodge against an argument, the defense of whose premisses took me into extended discussions of such recondite and profound subjects as Cantorian set theory, transfinite arithmetic, the ontological status of sets, the nature of time as tensed or tenseless, Zeno's Paradoxes, Kant's First Antinomy, contemporary Big Bang cosmology (including critiques of alternative or non-standard cosmological theories such as the Steady State model, the Oscillating model, the Vacuum Fluctuation model, and Quantum Gravity models), thermodynamics and physical eschatology, and so on and so forth.{3} Although the over-all logic of the argument is extremely simple, establishing the truth of its premisses can be, depending upon the depth to which one wishes to go, a long and complex affair, involving not only the issues mentioned above, but also additional argumentation to rule out such hypotheses as an eternally quiescent universe in which the temporal series of past events was initiated.{4} Moreover, the simple syllogism lying at the heart of the kalam cosmological argument should be supplemented by a conceptual analysis of what it is to be a cause of the universe, an exercise which serves to recover many of the traditional divine attributes, demonstrating that the inferred cause of the universe is an uncaused, beginningless, timeless, changeless, spaceless, immaterial, personal Creator of unimaginable power. So although the kalam cosmological argument has the virtue of being formulable in a simple syllogism, the appearance of swiftness and simplicity which this apparently engenders in some should not lead one mistakenly to infer that the argument is simplistic or cursory in its treatment of difficult questions.
It is worth noting that Taylor does not dispute the truth of the argument's two premisses. Indeed, he rejects any attempt to deny the first premiss, that whatever begins to exist has a cause, and it is my impression that he may well accept the truth of the second as well. So he does not deny the soundness of the argument; rather he offers undercutting defeaters of the second premiss in order to show that the proponent of the argument has not been successful in his attempt to provide adequate warrant for believing the second premiss to be true.
I think I can show, however, that it is Taylor who is far too quick and easy in his critique. For several of his objections have already been dealt with in the literature, and yet he takes no cognizance of the answers; other arguments on behalf of main premiss of the kalam cosmological argument he simply ignores.
II. Philosophical Arguments
Taylor attempts to refute what he calls a priori arguments (but which might more accurately be called philosophical or metaphysical arguments, since they do, pace Taylor, involve appeal to experience) for the beginning of the universe. With respect to the first of these, the argument based on the impossibility of the existence of an actual infinite, we immediately encounter a misconstrual of the argument: Taylor characterizes the argument as "claiming to show that the proposition that something could be actually infinite implies a contradiction"{5} --this despite my oft-repeated statements that the argument does not rest on any such claim.{6} Rather the argument purports to make it plausible that the existence of an actual infinite is metaphysically impossible. Compare in this connection such statements as "Some effect occurs before its cause," "Something has a shape but not a size," or "Something comes into being without a cause"--statements which imply no contradiction, but which are, plausibly, metaphysically impossible. Similarly, the statement that "an actual infinite exists" may imply no contradiction and yet be metaphysically impossible.
Taylor offers both an undercutting and a rebutting defeater of the premiss that an actual infinite cannot exist. First, in response to my argument that if an actually infinite number of things, say, books, could exist, then it would be impossible to add to the collection, which is obviously absurd, Taylor rejoins that one may simply re-number the collection so as to admit the addition of the new member.{7} But the shortcoming of this refutation lies in the fact that I had already anticipated this objection in the original statement of the problem and explained that such a re-numbering violates the problem conditions laid down and merely substitutes new conditions.{8} Unfortunately, Taylor takes no cognizance of my pre-emptive refutation of this objection. Worse, Taylor simply breaks off his discussion at this point, ignoring all the even more counter-intuitive absurdities entailed by the existence of an actual infinite, such as those illustrated by Hilbert's Hotel, including the contradictions which result when the inverse operations of subtraction or division are performed with transfinite numbers, operations which may be conventionally banned within transfinite arithmetic but which cannot be precluded in the real world of space and time.
Second, Taylor would rebut the premiss in question by furnishing a counter-example: the number of natural numbers is actually infinite.{9} In order to carry this objection, Taylor needs to address two subsidiary questions:
(i) Are there mathematical instances of actual infinites? That there are cannot simply be assumed, for intuitionist mathematicians--a small, but brilliant minority--deny the legitimacy of the notion of actual infinity even in the mathematical realm, accepting potential infinites only.{10} Taylor must show why the proponent of the kalam cosmological argument cannot rationally embrace intuitionism, a task which Taylor has not even begun to attempt--otherwise Taylor's objection is undercut.
(ii) What is the ontological status of mathematical entities? As I explained in The Kalam Cosmological Argument, only if one is a Platonist is the admission of mathematical actual infinities incompatible with the claim that an actual infinite cannot exist.{11} So long as Formalism, Conceptualism, or Nominalism remains a viable option, the kalam proponent need not deny the legitimacy of the mathematical actual infinite. Moreover, I pointed out that Platonism is peculiarly burdened with the antinomies of naive set theory, specifically Burali-Forti's antinomy, Cantor's antinomy, and Russell's antinomy. Further, I explained that the customary means of avoiding these paradoxes, such as logicism or axiomatization, sit ill with a metaphysic of Platonism.
Although Platonism seems very popular today among metaphysicians, I think there are good reasons, wholly independent of the kalam cosmological argument, for preferring some form of Conceptualism over Platonism:
(A) The entities postulated in a Platonist ontology are obscure. I must confess that, try as I might, I simply have no idea what the Platonist is talking about when he asserts, for example, that the number three exists. To say that it is an abstract object existing timelessly and spacelessly is not elucidating. I understand what it means to say there are three of something, three apples, say, and the concept of threeness is clear to me; but the notion that three itself exists is utterly opaque. What is the Platonist talking about when he asserts that independently of all conceptualization, even on the part of God, there exist these infinite realms of strange objects like numbers and sets and points and lines, et cetera?
(B) Platonism is theologically unacceptable.{12} The abstract objects posited in a Platonist ontology exist, to borrow Plantinga's phrase, just as serenely as your most solidly concrete object.{13} There are thus infinite upon infinite realms of necessarily existing objects--numbers, curves, n-dimensional geometries, propositions, properties, relations, essences, possible worlds, theories, musical scores, and so on and so forth--which exist independently of God. Platonism thus entails a metaphysical pluralism which compromises the aseity of God. Some theists have attempted to marry Platonism to theism by postulating a sort of absolute creation, according to which doctrine abstract objects do not exist a se, but are necessary creations of God.{14} Insofar as the means of such objects' creation is divine intellection, however, then this is actually a Conceptualist, not a Platonist, metaphysic. Construed, on the other hand, as creation by the divine will, Platonism remains theologically unacceptable, for it then denies divine freedom with respect to creation and emasculates the doctrine of creatio ex nihilo, since God co-exists eternally with creation, only the (infinitesimally small) physical part of creation coming into being at a point in time. Platonism is thus profoundly unacceptable theologically, such that even were I not convinced of the truth of the premisses of the kalam cosmological argument, I should reject Platonism in favor of Conceptualism.
On a Conceptualist ontology, numbers are products of intellection, ultimately divine intellection, as Plantinga explains:
It . . . seems plausible to think of numbers as dependent upon or even constituted by intellectual activity; indeed, students always seem to think of them as 'ideas' or 'concepts,' as dependent upon our intellectual activity. So if there were no minds, there would be no numbers . . . . But again, there are too many of them for them to arise as a result of human intellectual activity; we should therefore think of them as among God's ideas.{15}
But, it might be rejoined, does not Conceptualism merely push the problem back a notch, forcing us to posit an actually infinite number of divine ideas?{16} Not at all! In the first place, one need not be conceptualizing consciously all that one knows. I know, for example, the multiplication table up to 10 although I am not consciously entertaining any of its individual equations, so that my knowledge of the multiplication table does not imply that I have 102 ideas. Secondly, and more importantly, the Conceptualist may avail himself of the theological tradition that in God there are not, in fact, a plurality of divine ideas; rather God's knowledge is simple and is merely represented by us finite knowers as broken up into knowledge of discrete propositions and a plurality of divine ideas.{17} William Alston points out that such a doctrine of divine knowledge does not commit one to a full-blown doctrine of divine simplicity.{18} Such a full-blown doctrine faces well-known difficulties; but with respect to divine intellection such a simplicity doctrine has considerable advantages independent of the concerns of the kalam cosmological argument. For example, it allows one to circumvent wholly Patrick Grimm's paradoxes of omniscience based on God's knowledge of individual truths.{19}
It seems to me, therefore, that there are substantive, independent reasons for rejecting Platonism. The detractor of the kalam cosmological argument thus finds himself shouldered with an enormous burden of proof if he is to carry his objection based on the existence of mathematical infinites: he must prove, first, that intuitionism is not a rationally tenable position and, second, that Platonism alone is a reasonable metaphysic with respect to abstract objects. Taylor has not even begun to discuss these issues. His refutation of the argument against the existence of an actual infinite is thus--shall I say it?--far too swift and simple.
Taylor also attempts to refute the premiss that an infinite temporal regress of events is an actual infinite. He observes that the series of past events is not like an infinite set of books in a library, for, in contrast to the books, "there would seem to be no clear sense in which the series of past events may be said to exist all at once."{20} Notice that the difficulty here lies not in the difference between events and things, but in the difference between entities, some of which are past, and entities, all of which are present. The assumption seems to be that if a series or collection has a cardinality, then all the members of that collection must exist simultaneously. But that seems patently false: does not the series of U.S. presidents have, as of 1999, 42 members? If the series were beginningless, would it not have 
0 members? Certain thinkers have tried to avoid that conclusion by contending that the number of members of such a series would be merely potentially infinite.{21} But this contention is clearly wrong; since the series has an end in the present, in order to be potentially infinite the series would, as of that date, have to be finite but growing in a backward direction, which is absurd. If there were a beginningless series of falling dominoes, would not the number of dominoes fallen prior to today be actually infinite? How, then, would the number of fallen dominoes be different if each one, after falling, eventually decayed and ceased to exist?
Perhaps Taylor's objection is, not that the number of past events in a beginningless universe is not actually infinite, but that an actually infinite number of things which exist successively, not simultaneously, does not engender the alleged absurdities attending a simultaneously existing number of things. But this contention is obviously false: we can still compare, for example, the number of odd-numbered events with the total number of events, or the number of events prior to today with the number of events prior to any point in the past, and mentally add and subtract such events so as to obtain the same absurdities. In fact, the successive existence of the collection of past events affords striking illustrations of the counter-intuitive nature of the actual infinite: for example, the number of respective revolutions completed by two concentric spheres rotating at a 1:12 ratio will increasingly diverge the longer they revolve; but if they have revolved long enough, they will have miraculously completed the same number of revolutions! Indeed, appeal to the successive nature of the existence of past events lands one in the second, independent kalam argument against the formation of an actual infinite by successive addition, so that we are, in effect, presented with a dilemma, as Davis discerns:{22}
(i) If the series of past events is beginningless, then it constitutes either a simultaneously existing actual infinite or a series formed by successive addition.
(ii) It cannot be a simultaneously existing actual infinite (first KCA).
(iii) It cannot be a series formed by successive addition (second KCA).
(iv) Therefore, the series of events is not beginningless.
Thus, even if the first kalam argument were inappropriate (which is moot), still the second argument would suffice to demonstrate the finitude of the past.
Turning, then, to the second kalam argument for the beginning of the universe, we find Taylor offering a critique of my Tristram Shandy paradox which I admitted in Theism, Atheism, and Big Bang Cosmology to be quite justified.{23} I had initially argued that Tristram Shandy, who writes his autobiography so slowly that it takes him a year to record the events of a single day, would, had he been writing from eternity past, have completed his autobiography by today, since, by the Principle of Correspondence, there has been a year available for writing corresponding to every day of living; but such a conclusion is absurd, since he could not yet have recorded today's events. Critics of the argument pointed out, however, that the absurdity of the Tristram Shandy story lies not in the infinity of the past, but in the requirement that he record a day not succeeded by a year. He can only record days which are earlier than the corresponding years of writing, no matter how briefly he has lived. The task assigned to Tristram Shandy is impossible, as Taylor says, "for reasons that have nothing to do with the actual infinite."{24} Therefore, if the past is infinite, there is no reason to think that he will have recorded today's events.
But then, as I pointed out, the obvious question arises: if Tristram Shandy has been writing from eternity, which days has he recorded? As Robin Small's incisive analysis reveals, the days recorded by Tristram Shandy must be infinitely distant in the past. For given that every year of writing is preceded by the relevant recorded day and that the number of years is infinite, the recorded days must be infinitely distant from the present. But this seems absurd, since, as G. J. Whitrow argued, it is impossible for an event which was once present to recede to an infinite temporal remove. But since the task of writing one's autobiography at the rate of one day a year (such that the year comes after the day recorded) is an obviously possible task, an actually infinite past must be impossible.
Taylor does not seem to grasp this revised paradox, merely repeating Small's contention that the days recorded and the years of writing cannot be put into a one-to-one correspondence. This is obviously false, since both have the cardinality of 0. Since every day of living generated a year of writing, the days and years cannot fail to correspond. Thus, there is no logical problem in locating the days corresponding to the years: they exist in the w * series of days preceding the w * series of years (. . . , -3, -2, -1, . . . , -3, -2, -1). Moreover, Taylor takes no cognizance of what I called a "deeper absurdity" revealed by the Tristram Shandy paradox, namely, that if Tristram Shandy were going to finish his book by the present moment, then he would always at any moment in the past have already completed it.{25} Thus, Taylor's treatment of the second kalam cosmological argument, like that of the first, is all too quick and easy.{26}
In summary, Taylor's refutation of the philosophical arguments for the beginning of the universe cannot be deemed successful, first, because his examination of the arguments is simply incomplete, and, second, with respect to those arguments which he does treat, Taylor's defeaters are based on misinterpretations, mistakes, or inadequate exploration of alternatives.
III. Scientific Confirmations
We now come to the scientific confirmation of the philosophical arguments for the beginning of the universe. Taylor admits that if it could be "shown satisfactorily that the universe began ex nihilo, from no prior cosmological goings-on, then the only available causes would be supernatural."{27} Now it needs to be understood clearly that this is precisely what the standard Big Bang theory, if true, does show. The initial cosmological singularity constitutes the boundary to physical time and space, so that if the theory is true, we have an origin of the universe ex nihilo. As Barrow and Tipler state, "At this singularity, space and time came into existence; literally nothing existed before the singularity, so, if the Universe originated at such a singularity, we would truly have a creation ex nihilo."{28} Thus, if the model provides a realistic description of the universe, there cannot be physical causal conditions of the Big Bang. As Grünbaum emphasizes, to postulate a physical cause of the Big Bang is simply to contradict the theory.{29}
Now Taylor seems to recognize the above implication of the standard model, and so he is compelled to argue, in effect, that if we construe the Big Bang model realistically, we must reject the Big Bang theory as false. That Taylor does, in fact, affirm this stringent claim is evident from the following argument:
The prediction, by a theory, of a singularity, is standardly taken as evidence that the theory has broken down. In the cosmological case, it indicates that there is an era in the universe's history about which we cannot rely on the Big Bang's predictions. The Big Bang theory is not telling us that the universe had an absolute beginning. The correct conclusion to be drawn from the singularity is that the theory does not tell us what happened in the earliest phase of the universe.{30}
In Taylor's thinking, the prediction on the part of the Big Bang theory of an initial cosmological singularity is proof positive that the theory is wrong.
Now it is certainly true that theorists prefer a theory which involves no singularities, since the laws of physics break down at such a point; but that heuristic does nothing to rule out the fact that the correct theory of the universe may well involve singularities. The Hawking-Penrose singularity theorem proves that so long as the General Theory of Relativity holds, an initial cosmological singularity is inevitable. A singular beginning of the universe is not ipso facto unphysical or unscientific, though it may be discomfiting. A theorist is always at liberty, if he has an aversion to singularities, to "cut out" the initial singular point from the model, treating it, in Fitzgerald's words, "as a kind of mathematical limit lacking physical reality."{31} But the discomfiture of an absolute beginning remains unabated. As cosmologist Andrei Linde candidly confesses, "The most difficult aspect of this problem is not the existence of the singularity itself, but the question of what was before the singularity . . . . This problem lies somewhere at the boundary between physics and metaphysics."{32}
Taylor errs in inferring that the presence of an initial cosmological singularity implies an era about which the standard model's predictions are unreliable. The singular state is a durationless point with respect to time, the analogue to a temporal instant; t=0 does not even lie within the history of the universe, much less constitute an era, but lies on the boundary of space-time. Taylor seems to have confused the singular state with the Planck era prior to 10-43 sec after the Big Bang, whose description requires the marriage of GTR and quantum theory to yield a quantum theory of gravitation.{33} Some theorists hope that such a theory will not involve the singularities inevitable in classical gravitation; but this hope may well prove vain. John Barrow has rightly cautioned that "one should be wary of the fact that many of the studies of quantum cosmology are motivated by the desire to avoid an initial singularity of infinite density, so they tend to focus on quantum cosmologies that avoid a singularity at the expense of those that might contain one."{34} Noting the same tendency, Roger Penrose states, "I have gradually come around to the view that it is actually misguided to ask that the space-time singularities of classical relativity should disappear when standard techniques of quantum (field) theory are applied to them."{35} For if the initial cosmological singularity is removed, then "we should have lost what seems to me to be the best chance we have of explaining the mystery of the second law of thermodynamics."{36} What Penrose has in mind is the remarkable fact that as one goes back in time the entropy of the universe steadily decreases. Just how unusual this is can be demonstrated by means of the Bekenstein-Hawking formula for the entropy of a stationary black hole. The total observed entropy of the universe is 1088. Since there are around 1080 baryons in the universe, the observed entropy per baryon must be regarded as extremely small. By contrast in a collapsing universe the entropy would be 10123 near the end. Comparison of these two numbers reveals how absurdly small 1088 is compared to what it might have been. Thus, the structure of the Big Bang must have been severely constrained in order that thermodynamics as we know it should have arisen. So how is this special initial condition to be explained? According to Penrose, we need the initial cosmological singularity, conjoined with the Weyl Curvature Hypothesis, according to which initial singularities (as opposed to final singularities) must have vanishing Weyl curvature.{37} In standard models, the Big Bang does possess vanishing Weyl curvature. The geometrical constraints on the initial geometry have the effect of producing a state of very low entropy. So the entropy in the gravitational field starts at zero at the Big Bang and gradually increases through gravitational clumping. The Weyl Curvature Hypothesis thus has the time asymmetric character necessary to explain the second law. Without the initial singularity we should have white holes spewing out material, in contradiction to the Weyl Curvature Hypothesis, the Second Law of Thermodynamics, and probably also observation.{38} Penrose supplies the following figure to illustrate the difference:
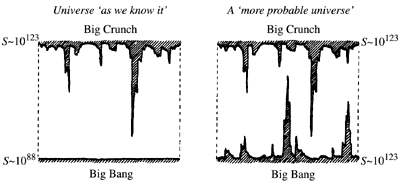
Fig. 1. Contrast between the universe as we know it (assumed for convenience to be closed) with a more probable universe. In both cases the Big Crunch is a high entropy (~10123), complicated, unconstrained singularity. For the left-hand picture the Big Bang is a low entropy (< 10), highly constrained, initial singularity, while for the right-hand picture it is an unconstrained, much more probable Big Bang. The "stalactites" represent singularities of black holes, while the "stalagmites" represent singularities of white holes.
If we remove the initial cosmological singularity, we render the Weyl Curvature Hypothesis irrelevant and "we should be back where we were in our attempts to understand the origin of the second law."{39} Could the special initial geometry have arisen sheerly by chance in the absence of a cosmic singularity? Penrose's answer is decisive: "Had there not been any constraining principles (such as the Weyl curvature hypothesis) the Bekenstein-Hawking formula would tell as that the probability of such a 'special' geometry arising by chance is at least as small as about one part in 101000B(3/2) where B is the present baryon number of the universe [~1080]."{40} Thus Penrose calculates that, aiming at a manifold whose points represent the various possible initial configurations of the universe, "the accuracy of the Creator's aim" would have to have been one part in 1010(123) in order for our universe to exist.{41} He comments, "I cannot even recall seeing anything else in physics whose accuracy is known to approach, even remotely, a figure like one part in 1010 (123)."{42}
Furthermore, the fact that certain quantum gravity models like the Hartle-Hawking model lack an initial singular point is in any case really quite irrelevant to our concern, since such models still posit the finitude of the past and an origination of the universe ex nihilo. As Barrow explains, "This type of quantum universe has not always existed; it comes into being just as the classical cosmologies could, but it does not start at a Big Bang where physical quantities are infinite . . . ."{43} The Hartle-Hawking universe thus gives "a picture of 'creation out of nothing'," even though "one never runs into an unusual point like the apex of a cone."{44}
Thus, Taylor's claim that the presence of an initial cosmological singularity in the standard model necessitates anti-realism with regard to that model is simply wrong. Nor does the necessity of a quantum theory of gravity to describe the Planck era imply abnegation of the initial cosmological singularity or, in any case, serve to avert the beginning of the universe. According to Hawking in his most recent book, "almost everyone now believes that the universe, and time itself, had a beginning at the Big Bang."{45} The defender of the kalam cosmological argument can hardly be indicted for appealing to this vast consensus in support of his argument.
Taylor also makes a more modest claim in an attempt to undercut the confirmation from Big Bang cosmology enjoyed by the kalam cosmological argument, namely, one may abjure a realist construal of the Big Bang model. But on what grounds should we doubt a realist interpretation of the model? Taylor answers, "The heart of the case against realism lies in the possibility of underdetermination of theories by the data, that is, the possibility that, alongside a successful theory, there may be another, incompatible theory, which equally well accounts for the available data."{46} Now insofar as Taylor has reference to scientific theories in general, he is correct that the practitioner of kalam, in appealing to the Big Bang theory in support of the second premiss of his argument, does run up against the challenge of scientific anti-realism. But since such anti-realism afflicts all our scientific theorizing about the external world, calling into question the existence of even such theoretical entities as dinosaurs and other galaxies, it is no deficiency of the Big Bang model in particular. The natural theologian who is a scientific realist may simply consider himself in good company and relax unless and until some reason is proffered for anti-realism about the Big Bang theory in particular. Taylor seems to sense the deficiency of broad-brush anti-realism and goes on to suggest that it is not implausible that there could be some empirically equivalent rival to the Big Bang theory which does not involve a beginning of the universe. I see no reason to dispute that that could be the case; but surely the mere possibility of such a theory is not sufficient justification for anti-realism about the Big Bang theory in particular. Taylor does not seem to appreciate how arduously detractors of the standard model have sought for such a theory and how extraordinarily difficult it has proved to find one. He is no doubt aware of the demise of the old Steady State theory. But he continues to speak favorably of oscillating models and of vacuum fluctuation models,{47} apparently unaware of the severe theoretical and observational difficulties which have rendered such theories obsolete.{48} Just this year five teams of astronomers at Princeton, Yale, the Lawrence Berkeley National Laboratory, and the Harvard-Smithsonian Center for Astrophysics, employing different measurement techniques, confirmed earlier results indicating that the density of the universe is insufficient to halt the expansion of the universe and bring about a contraction, thereby precluding an oscillating universe.{49} As for vacuum fluctuation models, Christopher Isham notes that such models encountered "fairly lethal" difficulties concerning their observational consequences and so were "jettisoned twenty years ago."{50} So what other prospective theories are there? Borde and Vilenkin have recently shown that Linde's attempt to craft a beginningless inflationary universe shatters: "A physically reasonable spacetime that is eternally inflating to the future must possess an initial singularity. The fact that inflationary spacetimes are past incomplete forces one to address the question of what, if anything, came before."{51} Taylor himself admits that the spacetimes of quantum gravity models like the Hartle-Hawking model cannot be interpreted as realistic alternatives to the standard model in view of their use of so-called imaginary time. Hawking himself is an anti-realist about his model: "The actual saddle point metric will be complex. This may upset a Platonist . . . but it is fine for a positivist like me."{52} "I don't demand that a theory correspond to reality because I don't know what it is. All I'm concerned with is that the theory should predict the results of measurements."{53} So where are these prospective theories that undercut realism with respect to the Big Bang theory?
Actually, there is one theory which does meet the criterion of accounting equally well for the empirical data and which should therefore occasion the suspicion that the standard model does not provide a realistic account of the spacetime universe, though this alternative account is one which is apt to come as a surprise to most people: Newtonian physics. E. A. Milne and W. H. McCrea shocked the scientific community by demonstrating that all the results of GTR-based Friedman cosmology can be recovered by Newtonian physics and in a way that is simpler than Einstein's cumbersome tensor calculus! Milne and McCrea were able to reproduce all the results of Big Bang cosmology by means of a material universe expanding in empty, classical space through classical time.{54} Schücking points out that the main asset of the Milne-McCrea formulation was that it gave exactly the same equations for the time development of the universe as the Friedman theory and yet allowed a much simpler derivation.{55} Comparing relativistic and Newtonian cosmology, Kerszberg observes, "as far as the prediction of the overall history of the universe is concerned, the equivalence seems to be total."{56} This implies, in Bondi's words, that GTR "cannot be expected to explain any major features in any different or better way than Newtonian theory."{57} As one who is philosophically attracted to Newtonian conceptions of time and space, I am not being facetious when I say that a cosmogonic theory based on Newtonian physics rather than Einstein's GTR constitutes a very real reason for doubting whether the origin of time and space postulated in the standard Friedman-LeMaître model of expanding space is not a fiction rooted in a now defunct positivistic epistemology. In the end, however, the success of Newtonian theory on a cosmological level remains merely a curiosity, since Newtonian physics is in contradiction with the evidence on the local level. Hence, the expansion of the universe is properly construed in Einsteinian terms as the expansion of space itself. So construed, there is no alternative theory which explains the data as well as a model predicting a beginning to physical space and time.
The history of the Big Bang model for well over three-quarters of a century has been one of radical predictions repeatedly confirmed and the repeated failure of every attempt, some of them extremely speculative, to avoid the absolute origin of the universe posited in the standard model.{58} With each failure, the theory is corroborated anew. The defender of the kalam cosmological argument seems to be on secure ground in appropriating the Big Bang theory as empirical confirmation of the beginning of the universe.
IV. Conclusion
In summary, then, it seems to me that the kalam cosmological argument meets reasonably suggested criteria for being a successful piece of natural theology. It is hard to deny that its premisses are at least more plausible than their contradictories. In particular, it seems more plausible to affirm, in light of philosophical argument and scientific confirmation, that the universe began to exist than that it did not begin to exist.
Taylor's attempt to undercut this premiss of the argument by defeating the philosophical arguments for the finitude of the past cannot be deemed a success. With respect to the first argument, based on the impossibility of the existence of an actual infinite, he misconstrues the nature of the modality involved, and his attempts to undercut and rebut the key premiss, that an actual infinite cannot exist, fail due to his ignoring both positive arguments offered in defense of the premiss as well as alternative positions open to the argument's defender which do not involve the existence of an actually infinite number of mathematical objects; moreover, his apparent denial of the second premiss, that an infinite temporal regress of events is an actual infinite, rests on confusion and forces Taylor into a dilemma, each horn of which implies the beginning of the universe. As for the second philosophical argument, based on the impossibility of the formation of an actual infinite by successive addition, Taylor's undercutting defeater is irrelevant to the version of the argument defended in Theism, Atheism, and Big Bang Cosmology; nor does he deal with the second consideration I offered in defense of impossibility of the successive formation of an actual infinite.
With regard to the empirical confirmation of the conclusion of the philosophical arguments, Taylor in effect admits that anyone who holds to a realist interpretation of the Big Bang theory should believe in God as the supernatural cause of the origin of the universe. For if that theory is correct in positing a beginning of the universe, then, since it is impossible for there to be physical antecedents of the Big Bang, it follows that we do have grounds "why positing a supernatural cause is more reasonable than positing a natural cause for the physical state in question."{59} The natural theologian who is a Big Bang realist is thereby exonerated, by Taylor's own lights, "from the charge of positing a 'God of the gaps'."{60} Thus, on Taylor's analysis to avoid God's existence one must be (not merely may be) an anti-realist concerning the Big Bang. I take this to be an enormous concession to the practitioner of kalam and to the power of his argument. Not many cosmologists would enjoy being forced into the dilemma of either being a theist or else an anti-realist. Moreover, we saw that Taylor's case for affirming anti-realism about the Big Bang was groundless and that, on the contrary, there exist good grounds for affirming the existence of an initial cosmological singularity.
In short, while the kalam cosmological argument enjoys the enormous heuristic advantage of being formulable in a simple syllogism, so that it can be easily communicated to a philosophically or scientifically untutored person, it is by no means simplistic and cannot be defeated by swift and simple objections.
Endnotes
{1}Stephen T. Davis, God, Reason, and Theistic Proofs, Reason and Religion (Grand Rapids, Mich.: Wm. B. Eerdmans, 1997), pp. 1-8.
{2}John Taylor, "Kalam: A Swift Argument from Origins to a First Cause?" Religious Studies 33 (1997): 167-179.
{3}See particularly William Lane Craig, The Kalam Cosmological Argument, Library of Philosophy and Religion (London: Macmillan, 1979); William Lane Craig and Quentin Smith, Theism, Atheism, and Big Bang Cosmology (Oxford: Clarendon Press, 1993).
{4}See William Lane Craig, "The Kalam Cosmological Argument and the Hypothesis of a Quiescent Universe," Faith and Philosophy 8 (1991): 104-108.
{5}Taylor, "Kalam," p. 168.
{6}See especially William Lane Craig, "Graham Oppy on the Kalam Cosmological Argument," Sophia 32 (1993): 1-3.
{7}Taylor, "Kalam," p. 169.
{8}Craig, Kalam Cosmological Argument, pp. 83-84; idem, Theism, Atheism, and Big Bang Cosmology, pp. 96-97.
{9}Taylor, "Kalam," pp. 169-170.
{10}See discussion in Craig, Kalam Cosmological Argument, pp. 92-94.
{11}Ibid., pp. 87-94.
{12}I realize that this point will have force only with theists. But I am quite interested in persuading fellow theists of the soundness of the kalam cosmological argument, both for the confirmation of their own faith and for the sake of evangelism. Even in dialogue with a non-theist, it is important to show that we can present a coherent conceptualist alternative to Platonism.
{13}Alvin Plantinga, The Nature of Necessity, Clarendon Library of Logic and Philosophy (Oxford: Clarendon Press, 1974), p. 132.
{14}See Thomas V. Morris and Christopher Menzel, "Absolute Creation," American Philosophical Quarterly 22 (1985): 353-362.
{15}Alvin Plantinga, "2 Dozen (or so) Theistic Arguments," lecture delivered at the 33rd Annual Wheaton College Philosophy Conference, October 23-25, 1986. See also idem, "How to Be an Anti-Realist," APA Proceedings and Addresses (1982): 47-70. Conceptualism thus affords a powerful argument for God's existence; see especially Quentin Smith, "The Conceptualist Argument for God's Existence," Faith and Philosophy 11 (1994): 38-49.
{16}See objections of William F. Lawhead, "The Symmetry of the Past and Future in the Kalam Cosmological Argument," and Robert Prevost, "Classical Theism and the Kalam Principle," in The Logic of Rational Theism, ed. Wm. L. Craig and M. S. McLeod, Problems in Contemporary Philosophy 24 (Lewiston, N.Y.: Edwin Mellen, 1990), pp. 99-111, 113-125 respectively.
{17}See Thomas Aquinas Summa theologiae 1a. 15. See also remarks of William Mann, "Necessity," in A Companion to Philosophy of Religion, ed. Philip L. Quinn and Charles Taliaferro, Blackwell Companions to Philosophy (Oxford: Blackwell, 1997), p. 267.
{18}William Alston, "Does God Have Beliefs?" Religious Studies 22 (1986): 287-306.
{19}Patrick Grimm, "Truth, Omniscience, and the Knower," Philosophical Studies 54 (1988): 9-41; Patrick Grimm and Alvin Plantinga, "Truth, Omniscience, and Cantorian Arguments: an Exchange," Philosophical Studies 71 (1993): 267-306.
{20}Taylor, "Kalam," p. 170.
{21}Thomas Aquinas Summa theologiae 1a. 7. 4; R. G. Swinburne, "The Beginning of the Universe," The Aristotelian Society 40 (1966): 131-132.
{22}Davis, God, Reason, and Theistic Proofs, p. 154.
{23}Craig and Smith, Theism, Atheism, and Big Bang Cosmology, p. 100.
{24}Taylor, "Kalam," p. 171.
{25}Craig and Smith, Theism, Atheism, and Big Bang Cosmology, pp. 104-106.
{26} Even quicker and easier is the treatment of the argument by Nicholas Everitt, "Interpretations of God's Eternity," Religious Studies 34 (1998): 25-32. According to Everitt, the "central error" of the argument is "the insistence on interpreting talk of infinity in terms of such empirical concepts such as those of traversing, or completing a movement"; rather the "correct understanding" recognises that "the infinity of a set of past times or past events consists in a relationship between the set and a proper subset", which "is not a relationship which we have to create by counting, traversing, moving, etc." (Ibid., p. 32). Defenders of the kalam cosmological argument realise well that the correspondence relation in terms of which infinite sets are defined is tenseless, but the point is that on a tensed view of time (which this version of the argument presupposes) the series of past events does have to be created by successive addition, which is directly analogous to counting, traversing, etc. The question is whether an infinite series of events, having no beginning and having an ending in the present, is metaphysically possible given a tensed view of time. Intuitively, this does not seem possible, for it seems that the present event could not arrive if its arrival had to be preceded by the successive arrival of an infinite number of prior events. Everitt merely asserts that such a successive completion of the past is "certainly possible" (Ibid., p. 28), but only because the past's being infinite entails its having no beginning--which is not in dispute. He says nothing about my proffered arguments for the impossibility of such a series; indeed, he admits that if there were infinitely distant events (as Small's analysis of the Tristram Shandy paradox reveals), then there "would indeed be an absurdity" in the postulation of an infinite past (Ibid.).
{27}Taylor, Kalam," p. 174.
{28}John Barrow and Frank Tipler, The Anthropic Cosmological Principle (Oxford: Clarendon Press, 1985), p. 442.
{29}Adolf Grünbaum, "Creation as a Pseudo-Explanation in Current Physical Cosmology," Erkenntnis 35 (1991): 238-239.
{30}Taylor, "Kalam," p. 174.
{31}Paul Fitzgerald, "Swinburne's Space and Time," Philosophy of Science 43 (1976): 636; see further Craig and Smith, Theism, Atheism, and Big Bang Cosmology, pp. 226-227.
{32}Andrei Linde, "The Inflationary Universe," Reports on Progress in Physics 47 (1984): 976.
{33} The most promising candidate for such a unified theory is string theory, which construes fundamental entities, not as particles, but as strings and which has gravity as an inevitable consequence of the theory. On recent advances in this field see Edward Witten, "The Holes Are Defined by the String," Nature 383 (19 September, 1996), pp. 215-216; James Glanz, "Strings Unknot Problems in Particle Theory, Black Holes," Science 276 (27 June, 1997), pp. 1969-1970; Andrew Strominger and Cumrun Vafa, "Microscopic Origin of the Bekenstein-Hawking Entropy," Physics Letters B 379 (1996): 99-104.
{34}John Barrow, The Origin of the Universe (New York: Harper Collins, 1994), p. 113.
{35}Roger Penrose, "Some Remarks on Gravity and Quantum Mechanics," in Quantum Structure of Space and Time, ed. M. J. Duff and C. J. Isham (Cambridge: Cambridge University Press, 1982), p. 4.
{36}Ibid., p. 5.
{37}Weyl curvature is the curvature of space-time which is not due to the presence of matter and is described by the Weyl tensor. Space-time curvature due to matter is described by the Einstein tensor. Together they make up the Riemann tensor giving the metric for space-time.
{38}Stephen Hawking and Roger Penrose, The Nature of Space and Time, The Isaac Newton Institute Series of Lectures (Princeton, N. J.: Princeton University Press, 1996), p. 130.
{39}Penrose, "Remarks," p. 5.
{40}Ibid.
{41}Roger Penrose, "Time Asymmetry and Quantum Gravity," in Quantum Gravity 2, ed. C. J. Isham, R. Penrose, and D. W. Sciama (Oxford: Clarendon Press, 1981), p. 249; cf. Hawking and Penrose, Nature of Space and Time, pp. 34-35.
{42}Penrose, "Time Asymmetry," p. 249.
{43}John D. Barrow, Theories of Everything (Oxford: Clarendon Press, 1991), p. 68.
{44}Ibid., pp. 66, 67.
{45}Hawking and Penrose, Nature of Space and Time, p. 20.
{46}Taylor, "Kalam," p. 172.
{47}Ibid., p. 173.
{48}See objections to both in Craig and Smith, Theism, Atheism, and Big Bang Cosmology.
{49}"Studies Find Universe Will Expand Forever and Not Collapse," Associated Press News Release, 9 January 1998.
{50}Christopher Isham, "Space, Time, and Quantum Cosmology," paper presented at the conference "God, Time, and Modern Physics," March, 1990; idem, "Quantum Cosmology and the Origin of the Universe," paper presented at the conference "Cosmos and Creation," Cambridge University, July 14, 1994.
{51}Arvind Borde and Alexander Vilenkin, "Eternal Inflation and the Initial Singularity," Physical Review Letters 72 (1994): 3305, 3307. Linde agrees with their judgement (A. Linde, Physical Review D 49 (1994): 1783-1826). This is significant, since Linde's model is the only inflationary scenario not plagued with internal inconsistencies.
{52}Hawking and Penrose, Nature of Space and Time, p. 123. Complex quantities involve imaginary numbers.
{53}Ibid., p. 121.
{54}E. A. Milne, Relativity, Gravitation and World Structure (Oxford: Clarendon Press, 1935); idem, "A Newtonian Expanding Universe," Quarterly Journal of Mathematics 5 (1934): 64-72; W. H. McCrea, "On the Significance of Newtonian Cosmology," Astronomical Journal 60 (1955): 271-274.
{55}E. L. Schücking, "Newtonian Cosmology," Texas Quarterly 10 (1967): 274.
{56}Pierre Kerszberg, "On the Alleged Equivalence between Newtonian and Relativistic Cosmology," British Journal for the Philosophy of Science 38 (1987): 349.
{57}H. Bondi, Cosmology, 2d ed. (Cambridge: Cambridge University Press, 1960), p. 89.
{58}The red shift anomalies noted by Rhook and Zangari, whom Taylor cites in an attempt to undercut the empirical warrant for the Big Bang theory, have been progressively resolved as measurements have been refined; and Hoyle's attempt to explain the microwave background radiation as the result of the thermalization of starlight by condensed iron filaments in space is an ad hoc expedient of desperation which has commended itself to no one. Rhook and Zangari's main complaint is really with inflation--itself an attempt to explain away the fine-tuning of the Big Bang which is objectionable only to those who do not believe in an intelligent Designer of the universe.
{59}Taylor, "Kalam," p. 179.
{60}Ibid.
